Chapter 5

In this chapter and the chapter that follows, we explore the special structure of network models. This chapter focuses on the problems of product distribution.

The transportation problem is a special type of linear programming problem, where the objective is to minimize the cost of distributing a product from a number of sources to a number of destinations.

The transportation problem deals with a special class of linear programming problems in which the objective is to transport a homogeneous product manufactured at several plants (origins) to a number of different destinations at a minimum total cost. The total supply available at the origin and the total quantity demanded by the destinations are given in the statement of the problem. The cost of shipping a unit of goods from a known origin to a known destination is also given. Our objective is to determine the optimal allocation that results in minimum total shipping cost.

The transportation (or distribution) problem is significant for most commercial organizations that operate several plants and hold inventory in regional warehouses.

Mathematical Representation Of Transportation Problem

A firm has 3 factories - A, E, and K. There are four major warehouses situated at B, C, D, and M. Average daily product at A, E, K is 30, 40, and 50 units respectively. The average daily requirement of this product at B, C, D, and M is 35, 28, 32, 25 units respectively. The transportation cost (in Rs.) per unit of product from each factory to each warehouse is given below:

The problem is to determine a routing plan that minimizes total transportation costs.

Let x_ij = no. of units of a product transported from ith factory(i = 1, 2, 3) to jth warehouse (j = 1, 2, 3, 4).

It should be noted that if in a particular solution the x_ij value is missing for a cell, this means that nothing is shipped between factory and warehouse.

The problem can be formulated mathematically in the linear programming form as
Minimize = 6x₁₁ + 8x₁₂ + 8x₁₃ + 5x₁₄
+ 5x₂₁ + 11x₂₂ + 9x₂₃ + 7x₂₄
+ 8x₃₁ + 9x₃₂ + 7x₃₃ + 13x₃₄

subject to
Capacity constraints
x₁₁ + x₁₂ + x₁₃ + x₁₄ = 30
x₂₁ + x₂₂ + x₂₃ + x₂₄ = 40
x₃₁ + x₃₂ + x₃₃ + x₃₄ = 50

Requirement constraints
x₁₁ + x₂₁ + x₃₁ = 35
x₁₂ + x₂₂ + x₃₂ = 28
x₁₃ + x₂₃ + x₃₃ = 32
x₁₄ + x₂₄ + x₃₄ = 25

x_ij ³ 0

The above problem has 7 constraints and 12 variables.Since no. of variables is very high, simplex method is not applicable. Therefore, more efficient methods have been developed to solve transportation problems.

The general mathematical model may be given as follows

minimize c_ijx_ij

subject to

x_ij £ S_i  for i = 1,2, ....., m (supply)
x_ij ³ D_j  for j = 1,2, ....., n (demand)

x_ij ³ 0

For a feasible solution to exist, it is necessary that total capacity equals total requirements.
Total supply = total demand.
Or å a_i = å b_j.

If total supply = total demand then it is a balanced transportation problem. There will be (m + n – 1) basic independent variables out of (m x n) variables.

• Only a single type of commodity is being shipped from an origin to a destination.
• Total supply is equal to the total demand.
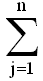  S_i = D_j
• S_i (supply) and D_j (demand) are all positive integers.