Assignment Problem: Linear Programming

The assignment problem is a special type of transportation problem, where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.

In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.

The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.

It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.

Formulation of an assignment problem

Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:

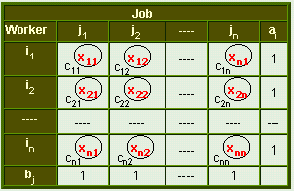
To formulate the assignment problem in mathematical programming terms, we define the activity variables as

xij =		1 if job j is performed by worker i
		0 otherwise

for i = 1, 2, ..., n and j = 1, 2, ..., n

In the above table, c_ij is the cost of performing jth job by ith worker.

Generalized Form of an Assignment Problem

The optimization model is

Minimize c₁₁x₁₁ + c₁₂x₁₂ + ------- + c_nnx_nn

subject to
x_i1 + x_i2 +..........+ x_in = 1          i = 1, 2,......., n
x_1j + x_2j +..........+ x_nj = 1          j = 1, 2,......., n

x_ij = 0 or 1

In Σ Sigma notation

minimize c_ijx_ij

subject to

x_ij = 1 for i = 1, 2, ....., n

x_ij = 1 for j = 1, 2, ....., n

x_ij = 0 or 1 for all i and j

Assumptions in Assignment Problem

• Number of jobs is equal to the number of machines or persons.
• Each man or machine is assigned only one job.
• Each man or machine is independently capable of handling any job to be done.
• Assigning criteria is clearly specified (minimizing cost or maximizing profit).