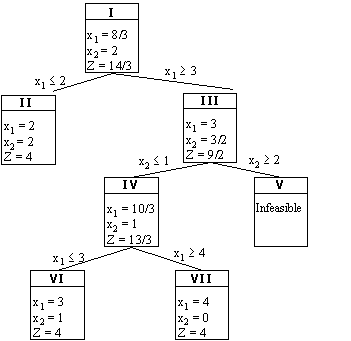
Branch and Bound Method Example
In the previous section, we listed steps in Branch and Bound Algorithm to solve an integer programming problem. In this section, we provide an example. Let's solve the following example:
 Example: Branch and Bound Method
Example: Branch and Bound Method
Maximize z = x1 + x2
subject to
3x1 + 2x2 ≤ 12
x2 ≤ 2
x1, x2 are integers ≥ 0
Solution.
First, we solve the above problem by applying the simplex method.
After introducing slack variables, we have
3x1 + 2x2 + x3 = 12
x2 + x4 =
2
where x3 and x4 are slack variables.
Initial basic feasible solution
x1 = 0, x2 = 0, and z = 0
x3 = 12, x4 = 2
Final Table
| cj | 1 | 1 | 0 | 0 | ||
|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x3 | x4 | Solution values b (=XB) |
| 1 | x1 | 1 | 0 | 1/3 | -2/3 | 8/3 |
| 1 | x2 | 0 | 1 | 0 | 1 | 2 |
| zj–cj | 0 | 0 | 1/3 | 1/3 |
x1 = 8/3, x2 = 2
Since the solution obtained is not an integer solution, we choose x1 = 8/3 (2 + 2/3), which has a fractional value and divide the problem
into the following two sub-problems (problem - II and problem - III) by adding two new constraints x1 ≤
2 & x1 ≥ 3, because [x1]
= [2 + 2/3] = 2.
Problem - II
Maximize z = x1 + x2
subject to
3x1 + 2x2 ≤ 12
x2 ≤ 2
x1 ≤ 2
x1, x2 ≥ 0
Introducing slack variables
3x1 + 2x2 + x5 = 12
x2 + x6 = 2
x1 + x7 = 2
where x5, x6 and x7 are slack variables.
Final Table
| cj | 1 | 1 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x5 | x6 | x7 | Solution values b (=XB) |
| 0 | x5 | 0 | 2 | 1 | 0 | -3 | 6 |
| 1 | x2 | 0 | 1 | 0 | 1 | 0 | 2 |
| 1 | x1 | 1 | 0 | 0 | 0 | 1 | 2 |
| zj–cj | 0 | 0 | 0 | 1 | 1 |
Optimal solution to problem - II is
x1 = 2, x2 = 2
Since all the variables in problem - II are integer valued, there is no need to branch this problem further.
Problem - III
Maximize z = x1 + x2
subject to
3x1 + 2x2 ≤ 12
x2 ≤ 2
x1 ≥ 3
x1, x2 ≥ 0
We use the two phase method to solve this problem.
Introducing slack, surplus & artificial variables
3x1 + 2x2 + x8 = 12
x2 + x9 = 2
x1 - x10 + A1 = 3
where:
x8 and x9 are slack variables.
x10 is a surplus variable.
A1 is an artificial variable.
Final Table
| cj | 1 | 1 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x8 | x9 | x10 | Solution values b (=XB) |
| 1 | x2 | 0 | 1 | 1/2 | 0 | 3/2 | 3/2 |
| 0 | x9 | 0 | 0 | -1/2 | 1 | -3/2 | 1/2 |
| 1 | x1 | 1 | 0 | 0 | 0 | -1 | 3 |
| zj–cj | 0 | 0 | 1/2 | 0 | 1/2 |
x1 = 3, x2 = 3/2
The solution obtained is not integer valued. Since [x2] =
[1 + 1/2] = 1, we divide the problem - III into two parts by
adding two new constraints x2 ≤
1 & x2 ≥ 2. Thus, we
form two sub-problems (problem - IV and problem - V).
Problem - IV
Maximize z = x1 + x2
subject to
3x1 + 2x2 ≤ 12
x2 ≤ 2
x1 ≥ 3
x2 ≤ 1
x1, x2 ≥ 0
We use the two phase method to solve this problem.
Introducing slack, surplus & artificial variables
3x1 + 2x2 + x11 = 12
x2 + x12 = 2
x1 - x13 + A1 = 3
x2 + x14 = 1
where:
x11, x12 & x14 are slack
variables.
x13 is a surplus variable.
A1 is an artificial variable.
Final Table
| cj | 1 | 1 | 0 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x11 | x12 | x13 | x14 | Solution values b (=XB) |
| 0 | x13 | 0 | 0 | 1/3 | 0 | 1 | -2/3 | 1/3 |
| 0 | x12 | 0 | 0 | 0 | 1 | 0 | -1 | 1 |
| 1 | x1 | 1 | 0 | 1/3 | 0 | 0 | -2/3 | 10/3 |
| 1 | x2 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| zj–cj | 0 | 0 | 1/3 | 0 | 0 | 1/3 |
x1 = 10/3, x2 = 1
Problem - V
Maximize z = x1 + x2
subject to
3x1 + 2x2 ≤ 12
x2 ≤ 2
x1 ≥ 3
x2 ≥ 2
x1, x2 ≥ 0
The solution to problem - V is infeasible. So we will not consider this problem.
But the solution to problem to problem - IV is not integer valued. Since [x1] = [3 + 1/3] = 3, we divide the problem - IV into two parts by adding two new constraints x1 ≤ 3 & x1 ≥ 4. Thus, we form two sub-problems (problem - VI and problem - VII).
Problem - VI
Maximize z = x1 + x2
subject to
3x1 + 2x2 ≤ 12
x2 ≤ 2
x1 ≥ 3
x2 ≤ 1
x1 ≤ 3
x1, x2 ≥ 0
Introducing slack, surplus & artificial variables
3x1 + 2x2 + x15 = 12
x2 + x16 = 2
x1 - x17 + A1 = 3
x2 + x18 = 1
x1 + x19 = 3
where:
x15, x16, x18 and x19 are
slack variables.
x17 is a surplus variable.
A1 is an artificial variable.
Final Table
| cj | 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x15 | x16 | x17 | x18 | x19 | Solution values b (=XB) |
| 0 | x15 | 0 | 2 | 1 | 0 | 0 | 0 | -3 | 3 |
| 0 | x16 | 0 | 1 | 0 | 0 | 0 | 0 | -1 | 2 |
| 1 | x1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 3 |
| 0 | x18 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | x17 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| zj–cj | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
This problem has multiple optimal solution. As x2 is zero, it enters into the basis.
The optimal solution is
x1 = 3, x2 = 1
Since all the variables in problem - VI are integer valued, there
is no need to branch this problem further.
Problem - VII
Maximize z = x1 + x2
subject to
3x1 + 2x2 ≤ 12
x2 ≤ 2
x1 ≥ 3
x2 ≤ 1
x1 ≥ 4
x1, x2 ≥ 0
Introducing slack, surplus & artificial variables
3x1 + 2x2 + x20 = 12
x2 + x21 = 2
x1 - x22 + A1 = 3
x2 + x23 = 1
x1 - x24 + A2 = 4
where:
x20, x21 and x23 are slack variables.
x22 and x24 are surplus variables.
A1 and A2 are artificial variables.
Final Table: Branch and Bound Method Example
| cj | 1 | 1 | 0 | 0 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|
| cB | Basic variables B |
x1 | x2 | x20 | x21 | x22 | x23 | x24 | Solution values b (=XB) |
| 1 | x2 | 0 | 1 | 1/2 | 0 | 0 | 0 | 3/2 | 0 |
| 0 | x21 | 0 | 0 | -1/2 | 1 | 0 | 0 | -3/2 | 2 |
| 1 | x1 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | 4 |
| 0 | x23 | 0 | 0 | -1/2 | 0 | 0 | 1 | -3/2 | 1 |
| 0 | x22 | 0 | 0 | 0 | 0 | 1 | 0 | -1 | 1 |
| zj–cj | 0 | 0 | 1/2 | 0 | 0 | 0 | 1/2 |
The optimal solution is
x1 = 4, x2 = 0
Since all the variables in problem - VII are integer valued, there is no need to branch this problem further.
The history of the complete branch and bound solution is displayed by means of the following tree like diagram.