Transportation Problem

Time Minimizing Problem

Succinctly, it is a transportation problem in which the objective is to minimize the time. This problem is same as the transportation problem of minimizing the cost, expect that the unit transportation cost is replaced by the time t_ij.

In a cost minimization problem, the cost of transportation depends on the quantity shipped. To the contrary, in a time minimization problem, the time involved is independent of the amount of commodity shipped.

"One thing you can't recycle is wasted time." -Anon.

Steps

1. Determine an initial basic feasible solution using any one of the following:

• North West Corner Rule
• Matrix Minimum Method
• Vogel Approximation Method

2. Find T_k for this feasible plan and cross out all the unoccupied cells for which t_ij ³ T_k.

3. Trace a closed path for the occupied cells corresponding to T_k. If no such closed path can be formed, the solution obtained is optimum otherwise, go to step 2.

Example 1

The following matrix gives data concerning the transportation times t_ij

Solution.

We compute an initial basic feasible solution by north west corner rule which is shown in table 1.

Table 1

Destination
Origin	D1	D2	D3	D4	D5	D6	Supply
O1				40	45	37	37
O2	30	25			40	20	22
O3	40	20	40			22	32
O4	25	24	50	27			14
Demand	15	20	15	25	20	10

Here, t₁₁ = 25, t₁₂ = 30, t₁₃ = 20, t₂₃ = 20, t₂₄ = 30, t₃₄= 35, t₃₅ = 45, t₄₅ =30, t₄₆ = 25

Choose maximum from t_ij, i.e., T₁ = 45. Now, cross out all the unoccupied cells that are ³ T1.
The unoccupied cell (O3D6) enters into the basis as shown in table 2.

Table 2

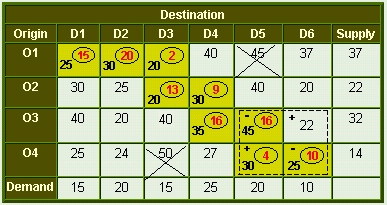
Choose the smallest value with a negative position on the closed path, i.e., 10. Clearly only 10 units can be shifted to the entering cell. The next feasible plan is shown in the following table.

Table 3

Destination
Origin	D1	D2	D3	D4	D5	D6	Supply
O1				40		37	37
O2	30	25			40	20	22
O3	40	20	40				32
O4	25	24		27		25	14
Demand	15	20	15	25	20	10

Here, T₂ = Max(25, 30, 20, 20, 20, 35, 45, 22, 30) = 45. Now, cross out all the unoccupied cells that are ³ T₂.

Table 4

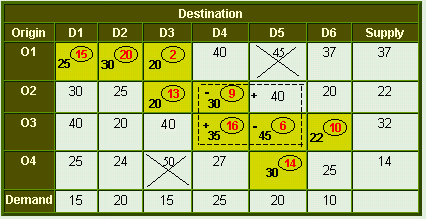
By following the same procedure as explained above, we get the following revised matrix.

Table 6

Destination
Origin	D1	D2	D3	D4	D5	D6	Supply
O1						37	37
O2	30	25				20	22
O3		20					32
O4	25	24		27		25	14
Demand	15	20	15	25	20	10

T₃ = Max(25, 30, 20, 20, 30, 40, 35, 22, 30) = 40. Now, cross out all the unoccupied cells that are ³ T₃.

Now we cannot form any other closed loop with T₃.
Hence, the solution obtained at this stage is optimal.
Thus, all the shipments can be made within 40 units.